《等式》等式与不等式PPT课时(第2课时一元二次方程的解集及其根与系数的关系)

《等式》等式与不等式PPT课时(第2课时一元二次方程的解集及其根与系数的关系)

第一部分内容：学 习 目 标

1.理解一元二次方程的定义，并会求一元二次方程的解集．(重点)

2．掌握一元二次方程的根的判别式，并会用其判断根的个数．(重点) 

3．掌握一元二次方程的根与系数的关系，并会用其求一些关于方程两根的代数式的值．(重点、难点)

核 心 素 养

1.通过对一元二次方程的解集及根与系数的关系的学习，培养数学抽象、逻辑推理的数学素养．

2．通过求一元二次方程的解集，提升数学运算素养.

... ... ...

等式PPT，第二部分内容：自主预习探新知

新知初探

1．一元二次方程的定义 

形如ax2＋bx＋c＝0的方程为一元二次方程，其中a，b，c是_______，且a≠0.

2．一元二次方程的解法 

(1)直接开平方法：利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法．

(2)配方法：通过方程的简单变形，将左边配成一个含有未知数的完全平方式，若右边是一个非负常数，则可以运用直接开平方法求解， 这种解一元二次方程的方法叫做配方法．

(3)公式法：将一元二次方程中的系数a，b, c的值代入式子x＝－b±b2－4ac2a中，就求得方程的根，这种解一元二次方程的方法叫做公式法．

3．一元二次方程根的判别式 

式子b2－4ac叫做一元二次方程ax2＋bx＋c＝0(a≠0)根的判别式，通常用Δ表示，即Δ＝b2－4ac.当Δ＞0 时，一元二次方程ax2＋bx＋c＝0(a≠0)有两个____的实数根；当Δ＝0时，一元二次方程ax2＋bx＋c＝0(a≠0)有两个____的实数根；当Δ＜0时，一元二次方程ax2＋bx＋c＝0(a≠0)____实数根．

4．一元二次方程的根与系数的关系 

如果ax2＋bx＋c＝0(a≠0)的两根是x1，x2，那么x1＋x2＝－ba，x1•x2＝ca，即两个根的和等于一次项系数与二次项系数的比的相反数，两个根的积等于常数项与二次项系数的比．

初试身手

1．一元二次方程x2－16＝0的解集是(　　)

A．{－8,8}　B．{－4}

C．{4}  D．{－4,4} 

2．用配方法解方程x2－8x＋5＝0，将其化为(x＋a)2＝b的形式，正确的是(　　)

A．(x＋4)2＝11  B．(x＋4)2＝21

C．(x－8)2＝11  D．(x－4)2＝11

3．用公式法解方程6x－8＝5x2时，a，b，c的值分别是(　　)

A．5、6、－8  B．5、－6、－8

C．5、－6、8  D．6、5、－8 

... ... ...

等式PPT，第三部分内容：合作探究提素养

一元二次方程的解法

角度一　直接开平方法

【例1】用直接开平方法求下列一元二次方程的解集：

(1)4y2－25＝0；(2)3x2－x＝15－x.

[思路点拨]　可将方程转化为x2＝p(p≥0)的形式．再两边开平方进行降次，化为一元一次方程．

规律方法

应用直接开平方法求一元二次方程解集的主要步骤

1化为x2＝pp≥0的形式；

2直接开平方；

3解两个一元一次方程，写出方程的两个根；

4总结写成解集的形式.

跟踪训练

1．用直接开平方法求下列一元二次方程的解集．

(1)(x＋1)2＝12；

(2)(6x－1)2－25＝0.

 角度二　配方法

【例2】　用配方法求下列方程的解集．

(1)x2＋4x－1＝0；

(2)4x2＋8x＋1＝0.

规律方法

利用配方法解一元二次方程ax2＋bx＋c＝0a≠0，先把二次项系数变为1，即方程两边都除以a，然后把常数项移到方程右边，再把方程两边加上一次项系数一半的平方，把方程的一边配方化为一个完全平方式，另一边化为非负数，然后用直接开平方法求解若另一边为负数，则此方程无实数根.

一元二次方程的根的判别式

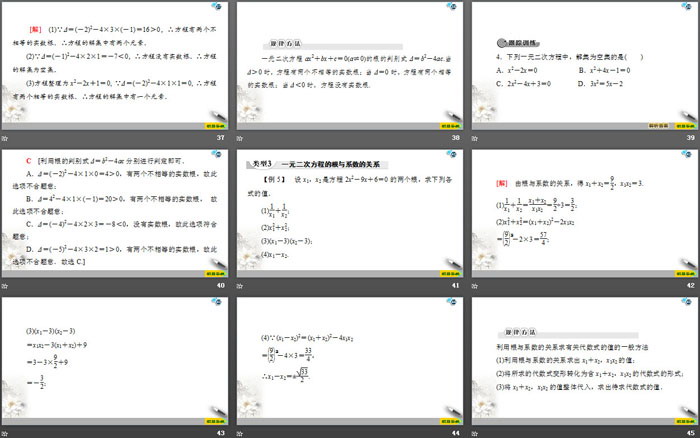
【例4】不解方程，判断下列一元二次方程的解集情况．

(1)3x2－2x－1＝0；

(2)2x2－x＋1＝0；

(3)4x－x2＝x2＋2.

[解](1)∵Δ＝(－2)2－4×3×(－1)＝16＞0，∴方程有两个不相等的实数根．∴方程的解集中有两个元素．

(2)∵Δ＝(－1)2－4×2×1＝－7＜0，∴方程没有实数根．∴方程的解集为空集．

(3)方程整理为x2－2x＋1＝0, ∵Δ＝(－2)2－4×1×1＝0, ∴方程有两个相等的实数根．∴方程的解集中有一个元素．

规律方法

一元二次方程ax2＋bx＋c＝0a≠0的根的判别式Δ＝b2－4ac.当Δ＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程没有实数根.

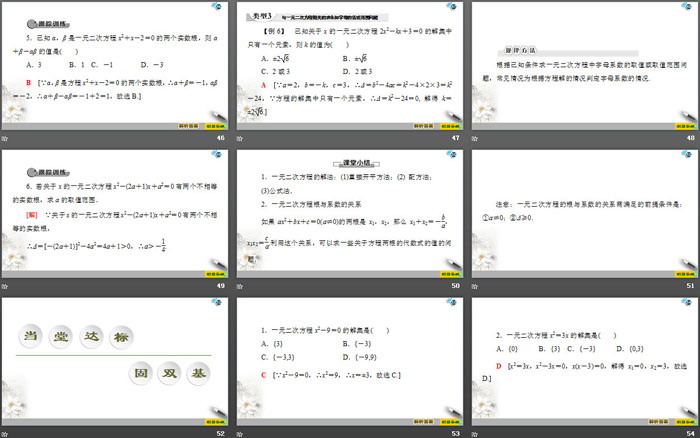
课堂小结

1．一元二次方程的解法：(1)直接开平方法；(2) 配方法；(3)公式法．

2．一元二次方程根与系数的关系

如果ax2＋bx＋c＝0(a≠0)的两根是x1，x2，那么x1＋x2＝－ba，x1x2＝ca.利用这个关系，可以求一些关于方程两根的代数式的值的问题．

注意：一元二次方程的根与系数的关系需满足的前提条件是：①a≠0；②Δ≥0.

... ... ...

等式PPT，第四部分内容：当堂达标固双基

1．一元二次方程x2－9＝0的解集是(　　)

A．{3}　　B．{－3}

C．{－3,3}  D．{－9,9} 

2．一元二次方程x2＝3x的解集是(　　)

A．{0}　B．{3}  C．{－3}　D．{0,3} 

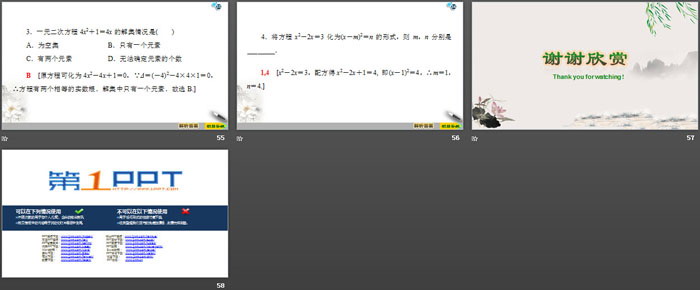
3．一元二次方程4x2＋1＝4x的解集情况是(　　)

A．为空集  B．只有一个元素

C．有两个元素  D．无法确定元素的个数 

4．将方程x2－2x＝3化为(x－m)2＝n的形式，则m，n分别是________．

... ... ...

关键词：高中人教B版数学必修一PPT课件免费下载，等式PPT下载，等式与不等式PPT下载，一元二次方程的解集及其根与系数的关系PPT下载，.PPT格式；

更多关于《 等式与不等式 等式 一元二次方程的解集及其根与系数的关系 》PPT课件, 请点击 等式与不等式PPT等式PPT一元二次方程的解集及其根与系数的关系PPT标签。

《一元一次不等式组》一元一次不等式和一元一次不等式组PPT(第2课时):

《一元一次不等式组》一元一次不等式和一元一次不等式组PPT(第2课时)，共16页。 第一部分内容：学习目标 熟练掌握解一元一次不等式组方法及在数轴上表示其解集; 运用一元一次不等式(..

《一元一次不等式组》一元一次不等式和一元一次不等式组PPT(第1课时):

《一元一次不等式组》一元一次不等式和一元一次不等式组PPT(第1课时)，共24页。 第一部分内容：学习目标 理解一元一次不等式组及其解的意义; 会解由两个一元一次不等式组成的不等式组..

《一元一次不等式与一次函数》一元一次不等式和一元一次不等式组PPT(第2课时):

《一元一次不等式与一次函数》一元一次不等式和一元一次不等式组PPT(第2课时)，共12页。 第一部分内容：学习目标 懂得一元一次不等式与一次函数的关系，会运用一次函数解决不等式的有..